Дано:
диагональ AC основания правильной четырехугольной пирамиды SABCD равна 6. Высота пирамиды SO равна 4.

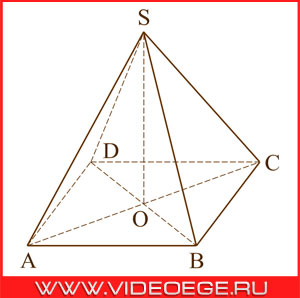
Вопрос:
найдите длину бокового ребра SB.

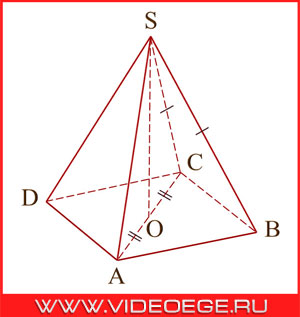
I этап: нахождение длины AO.

По свойству правильной пирамиды (боковые ребра правильной пирамиды равны):

SB = SC

Из определения правильной пирамиды следует, что ABCD – квадрат. Как известно, центром квадрата является точка пересечения его диагоналей. Причем диагонали квадрата ABCD точкой пересечения делятся пополам, следовательно:

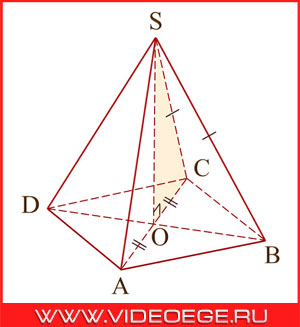
II этап: определение длины бокового ребра SB.

Рассмотрим ∆SOC. Он прямоугольный (∠SOC = 90°), так как SO –высота правильной пирамиды. 

По теореме Пифагора (в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов) применительно к треугольнику SOC:

SO² + OC² = SC²

Выразим из этого соотношения SC:

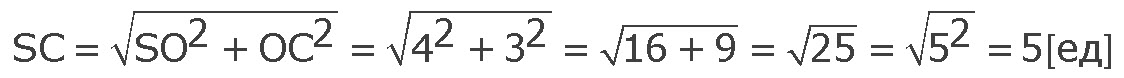
Так как SB = SC, то SB = 5 [ед].

1. определили длину AO. Расчет показал, что она равна 3 [ед];

2. детерминировали длину бокового ребра SB. Она составила 5 [ед].